|
Functions |
| int | elgv1sign (const mpbarrett *p, const mpbarrett *n, const mpnumber *g, randomGeneratorContext *, const mpnumber *hm, const mpnumber *x, mpnumber *r, mpnumber *s) |
| | This function performs raw ElGamal signing, variant 1.
|
| int | elgv3sign (const mpbarrett *p, const mpbarrett *n, const mpnumber *g, randomGeneratorContext *, const mpnumber *hm, const mpnumber *x, mpnumber *r, mpnumber *s) |
| | This function performs raw ElGamal signing, variant 3.
|
| int | elgv1vrfy (const mpbarrett *p, const mpbarrett *n, const mpnumber *g, const mpnumber *hm, const mpnumber *y, const mpnumber *r, const mpnumber *s) |
| | This function performs raw ElGamal verification, variant 1.
|
| int | elgv3vrfy (const mpbarrett *p, const mpbarrett *n, const mpnumber *g, const mpnumber *hm, const mpnumber *y, const mpnumber *r, const mpnumber *s) |
| | This function performs raw ElGamal verification, variant 3.
|
For more information on this algorithm, see: "Handbook of Applied Cryptography", 11.5.2: "The ElGamal signature scheme", p. 454-459
Two of the signature variants in Note 11.70 are implemented.
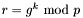
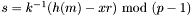
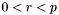 and
and 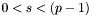
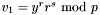
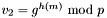
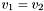
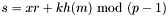
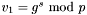
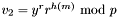
 1.3.6
1.3.6